チュートリアル：LIFニューロン Part1

第0週 1日目：Python Workshow 1

By Neuromatch Academy

コンテンツ作成者： Marco Brigham and the CCNSS team

コンテンツレビュアー： Michael Waskom, Karolina Stosio, Spiros Chavlis

エディター： Ella Batty, Spiros Chavlis

チュートリアルの目標

NMAでは、対話的な（そして、できれば楽しい）方法で計算神経科学を学ぶためにコードを使用します。このチュートリアルと次のチュートリアルは、コース前にPythonについて早めに理解するためのもので、コース中は計算神経科学の概念に焦点を当てることができます。

この章では、Pythonの変数、制御フロー、プロッティングの基本操作を練習し、Pythonの科学計算の主力であるnp.arrayについて確認します。

Pythonの新しい概念ごとに、Leaky Integrate-and-Fire (LIF) ニューロンの実装の異なる側面を学びます。そしてさらに良いことに、その膜電位の時間経過による変化を可視化し、その統計的特性を抽出します！

セットアップ

インストール

python

import numpy as np
import matplotlib.pyplot as plt

セクション1：Pythonの基礎とLIFモデル

ビデオ1：Pythonの基礎とLIFモデル

セクション1.1：LIFモデル

leaky-integrate-and-fire (LIF) ニューロンは、以下のような膜電位に関する方程式と初期化条件によって定義されます。

ここで、は膜電位、は膜の時定数、はリーク電位、は膜抵抗、はシナプス入力電流、は発火閾値、はリセット電圧を示します。また、膜電位についてはとも書くことができ、これはプロットのラベルに便利です。膜方程式は、シナプス入力と細胞膜を越えた電荷のリークに対する膜電位の時間変化を記述します。これは普通の微分方程式（ODE）で、これについては今後詳しく学んでいきます。

WARNING

このチュートリアルでは、ニューロンモデルは発火メカニズムを実装しないことに注意してください。

セクション1.2：コード中のコメント

ビデオ2：コメントと文字列に関する簡単な振り返り

コーディング演習1：パラメーターを定義する

まず、LIFニューロンの主なシミュレーション変数を定義し、初期化します。

以下のコードセルで、シミュレーションパラメータを出力するようにコードを修正してください。

python

# t_max = 150e-3   # second
# dt = 1e-3        # second
# tau = 20e-3      # second
# el = -60e-3      # milivolt
# vr = -70e-3      # milivolt
# vth = -50e-3     # milivolt
# r = 100e6        # ohm
# i_mean = 25e-11  # ampere

# print(t_max, dt, tau, el, vr, vth, r, i_mean)

出力例

0.15 0.001 0.02 -0.06 -0.07 -0.05 100000000.0 2.5e-10

それぞれの行の先頭の#を削除する必要がありました。そうしないと、コードはコメントとして読み取られ、実際には実行されません。コードを書くときには、デバッグのためにコードの一部を"コメントアウト"したい場合があるかもしれません。ここでは、数学的な記法に対応した説明的な変数名を使うようにしました。また、各行の末尾にコメントで単位を示しました。こうすることで、よりコードの意味を理解しやすくなります！

セクション1.3：数学的操作

コーディング演習2：入力電流をシミュレーションする

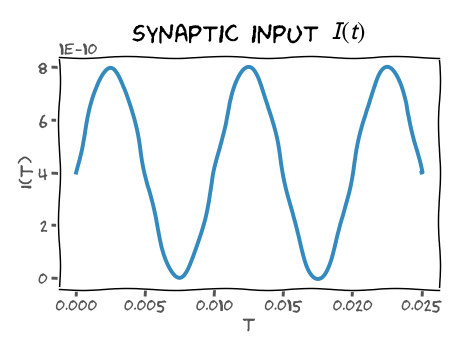
私たちのモデルニューロンに入力されるシナプス入力をシミュレートする必要があります。まず、この入力をシミュレートするためにsinモデルから始めます（上図）。その方程式は以下の通りです：

ここでは平均電流入力で、{t}は時間です。

次のセルでは、からまでの間のシナプス入力の値を計算します。ステップはです。

コーディング上の新しい概念

以下のコードではforループを使用します。後で詳しくforループについて説明しますが、基本的にforループは同じコードブロックを複数回実行できます。この場合、ステップをループし、それぞれの回で変数stepが新しい値となります。以下のような構文を使用します：

python

for step in range(10):

これは、stepが0から9までの各整数値を取ることを意味します。

np.piをの値として使用し、np.sin(x)を使用することでxのsinの値を取得できます。これらはnumpyというパッケージから来ており、後で詳しく説明します。

range関数

一般的に、range関数は、デフォルトで0から始まり、1ずつ増加し、指定した数の直前で止まる数列を返します。

Syntax

python

range(start, stop, step) # range(2, 10, 2) -> [2, 4, 6, 8]

Parameters:

start: オプショナル。どの位置から開始するかを指定する整数。デフォルトは0。
stop: 必須。どの値で停止するを指定する整数（stopの値自体は結果に含まれません）。
step: オプショナル。増加幅を指定する整数。デフォルトは1。

python

# Loop for 10 steps, variable 'step' takes values from 0 to 9
for step in range(10):

  # Compute value of t
  t = step * dt

  # Compute value of i at this time step
  i = ...

  # Print value of i
  print(i)

出力例

2.5e-10
3.969463130731183e-10
4.877641290737885e-10
4.877641290737885e-10
3.9694631307311837e-10
2.5000000000000007e-10
1.0305368692688176e-10
1.2235870926211617e-11
1.223587092621159e-11
1.0305368692688186e-10

セクション1.4：フォーマット済み文字列リテラル

フォーマット済み文字列リテラルトは、シミュレーションパラメータをきれいで整理された形で表示するのに便利です。Python 3.6では、新たな文字列フォーマットf-stringsが導入されました。私たちは浮動小数点型の変数を扱っているので、xを3桁の小数点までフォーマットするためにf'{x:.3f}'を使用し、4桁の小数点までフォーマットするために指数表記のf'{x:.4e}'を使用します。

python

x = 3.14159265e-1
print(f'{x:.3f}')
# --> 0.314

print(f'{x:.4e}')
# --> 3.1416e-01

コーディング演習3：綺麗な数値の表示

前の演習と同様にループを使って、の値を3桁の小数点、シナプス入力を指数表記の4桁の小数点で表示してください。

python

# Initialize step_end
step_end = 10

# Loop for step_end steps
for step in range(step_end):

  # Compute value of t
  t = step * dt

  # Compute value of i at this time step
  i = i_mean * (1 + np.sin((t * 2 * np.pi) / 0.01))

  # Print value of t and i
  print(...)

出力例

0.000 2.5000e-10
0.001 3.9695e-10
0.002 4.8776e-10
0.003 4.8776e-10
0.004 3.9695e-10
0.005 2.5000e-10
0.006 1.0305e-10
0.007 1.2236e-11
0.008 1.2236e-11
0.009 1.0305e-10

回答

python

# Initialize step_end
step_end = 10

# Loop for step_end steps
for step in range(step_end):

  # Compute value of t
  t = step * dt

  # Compute value of i at this time step
  i = i_mean * (1 + np.sin((t * 2 * np.pi) / 0.01))

  # Print value of t and i
  print(f'{t:.3f} {i:.4e}')

セクション2：`for`ループと離散時間積分

ビデオ3：`for`ループと離散時間積分

セクション2.1：`for`ループ

forループは、インデントされたコードブロックを複数回実行します（ループする変数は毎回新しい値になります）。以下の3つの形式はすべて同等であり、3回分ステップをループします：

python

# 1
for step in [0, 1, 2]:
  print(step)

# 2
for step in range(3):
  print(step)

# 3
start = 0
end = 3
stepsize = 1

for step in range(start, end, stepsize):
  print(step)

セクション2.2：スパイクによる離散時間積分

ビデオ4：離散時間積分の簡単な振り返り

次の演習では、十分に小さいを用いて、膜方程式の変化を離散的な時間ステップでシミュレートします。

まず、膜方程式の時間微分を、の極限を取らない形で記述します：

これを用いて、膜電位の値は、その前の値を用いて簡単な代数的操作で表すことができます。の値が十分に小さい場合、これは連続時間積分の良い近似値になります。

この操作が積分であり、ODEから一連のを得ることができます。ODEがの変化を直接的に記述しているわけではなく、の変化、つまりの微分の変化を記述しているという点に注意してください。の変化をシミュレーションするためには、ODEを積分する必要があります。このチュートリアルでは、オイラー法を使用して離散時間積分します。詳細は「常微分方程式の数値解法」を参照してください。

コーディング演習4：膜電位のシミュレーション

からの間のの変化を、ステップ幅との条件下で計算してください。

式（1）を変形して、左側にを分離し、と他の項の関数として表現する必要があります：

python

#################################################
## TODO for students: fill out compute v code ##
# Fill out code and comment or remove the next line
raise NotImplementedError("Student exercise: You need to fill out code to compute v")
#################################################

# Initialize step_end and v0
step_end = 10
v = el

# Loop for step_end steps
for step in range(step_end):
  # Compute value of t
  t = step * dt

  # Compute value of i at this time step
  i = i_mean * (1 + np.sin((t * 2 * np.pi) / 0.01))

  # Compute v
  v = ...

  # Print value of t and v
  print(f"{t:.3f} {v:.4e}")

出力例

0.000 -5.8750e-02
0.001 -5.6828e-02
0.002 -5.4548e-02
0.003 -5.2381e-02
0.004 -5.0778e-02
0.005 -4.9989e-02
0.006 -4.9974e-02
0.007 -5.0414e-02
0.008 -5.0832e-02
0.009 -5.0775e-02

回答

python

# Initialize step_end and v0
step_end = 10
v = el

# Loop for step_end steps
for step in range(step_end):
  # Compute value of t
  t = step * dt

  # Compute value of i at this time step
  i = i_mean * (1 + np.sin((t * 2 * np.pi) / 0.01))

  # Compute v
  v = v + dt/tau * (el - v + r*i)

  # Print value of t and v
  print(f"{t:.3f} {v:.4e}")

セクション3：プロッティング

ビデオ5：プロッティング入門

ビデオ6：プロッティングの簡単な振り返り

コーディング演習5：電流のプロット

この演習では、からの間のの値をプロットします。

まず、プロットのタイトルと軸のラベルを設定する必要があります。これらは説明的なラベルにしてください。その後、実際にプロットするためのコードを完成させる必要があります。

python

#################################################
## TODO for students: fill out the figure initialization and plotting code below ##
# Fill out code and comment or remove the next line
raise NotImplementedError("Student exercise: You need to fill out current figure code")
#################################################

# Initialize step_end
step_end = 25

# Initialize the figure
plt.figure()
plt.title(...)
plt.xlabel(...)
plt.ylabel(...)

# Loop for step_end steps
for step in range(step_end):

  # Compute value of t
  t = step * dt

  # Compute value of i at this time step
  i = i_mean * (1 + np.sin((t * 2 * np.pi) / 0.01))

  # Plot i (use 'ko' to get small black dots (short for color='k' and marker = 'o'))
  plt.plot(...)

# Display the plot
plt.show()

出力例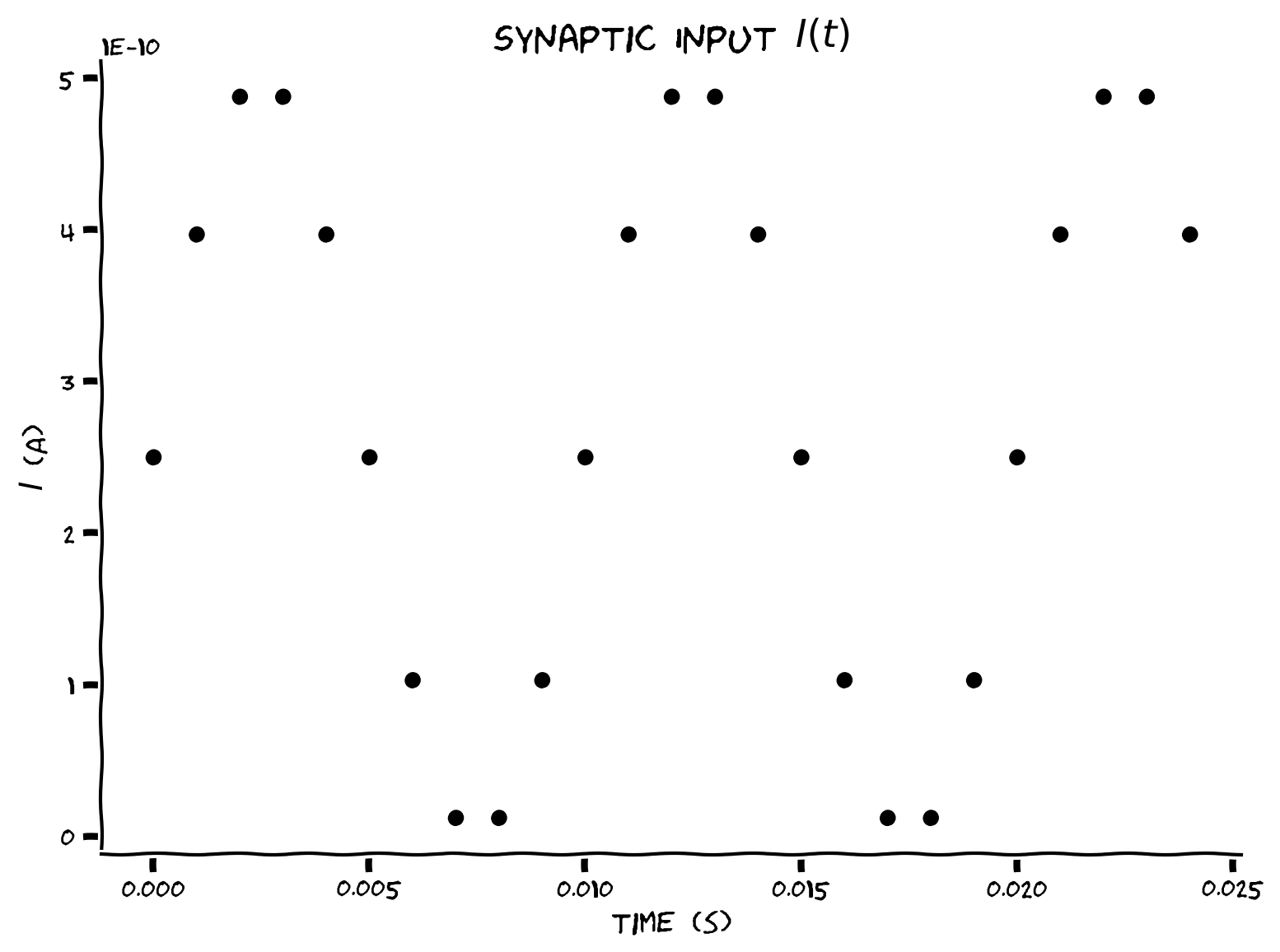 電流の時間変化のプロット例

回答

python

# Initialize step_end
step_end = 25

with plt.xkcd():
  # Initialize the figure
  plt.figure()
  plt.title('Synaptic Input $I(t)$')
  plt.xlabel('time (s)')
  plt.ylabel('$I$ (A)')

  # Loop for step_end steps
  for step in range(step_end):

    # Compute value of t
    t = step * dt

    # Compute value of i at this time step
    i = i_mean * (1 + np.sin((t * 2 * np.pi) / 0.01))

    # Plot i (use 'ko' to get small black dots (short for color='k' and marker = 'o'))
    plt.plot(t, i, 'ko')

  # Display the plot
  plt.show()

W0D1：Pythonワークショップ1

W0D2：Pythonワークショップ2

W1D1：モデルタイプ

W2D1：実践モデリング

チュートリアル：LIFニューロン Part1

チュートリアルの目標

セットアップ

インストール

セクション1：Pythonの基礎とLIFモデル

ビデオ1：Pythonの基礎とLIFモデル

セクション1.1：LIFモデル

セクション1.2：コード中のコメント

ビデオ2：コメントと文字列に関する簡単な振り返り

コーディング演習1：パラメーターを定義する

セクション1.3：数学的操作

コーディング演習2：入力電流をシミュレーションする

セクション1.4：フォーマット済み文字列リテラル

コーディング演習3：綺麗な数値の表示

セクション2：`for`ループと離散時間積分

ビデオ3：`for`ループと離散時間積分

セクション2.1：`for`ループ

セクション2.2：スパイクによる離散時間積分

ビデオ4：離散時間積分の簡単な振り返り

コーディング演習4：膜電位のシミュレーション

セクション3：プロッティング

ビデオ5：プロッティング入門

ビデオ6：プロッティングの簡単な振り返り

コーディング演習5：電流のプロット

チュートリアル：LIFニューロン Part1 ​

チュートリアルの目標 ​

セットアップ ​

インストール ​

セクション1：Pythonの基礎とLIFモデル ​

ビデオ1：Pythonの基礎とLIFモデル ​

セクション1.1：LIFモデル ​

セクション1.2：コード中のコメント ​

ビデオ2：コメントと文字列に関する簡単な振り返り ​

コーディング演習1：パラメーターを定義する ​

セクション1.3：数学的操作 ​

コーディング演習2：入力電流をシミュレーションする ​

セクション1.4：フォーマット済み文字列リテラル ​

コーディング演習3：綺麗な数値の表示 ​

セクション2：forループと離散時間積分 ​

ビデオ3：forループと離散時間積分 ​

セクション2.1：forループ ​

セクション2.2：スパイクによる離散時間積分 ​

ビデオ4：離散時間積分の簡単な振り返り ​

コーディング演習4：膜電位のシミュレーション ​

セクション3：プロッティング ​

ビデオ5：プロッティング入門 ​

ビデオ6：プロッティングの簡単な振り返り ​

コーディング演習5：電流のプロット ​

チュートリアル：LIFニューロン Part1

チュートリアルの目標

セットアップ

インストール

セクション1：Pythonの基礎とLIFモデル

ビデオ1：Pythonの基礎とLIFモデル

セクション1.1：LIFモデル

セクション1.2：コード中のコメント

ビデオ2：コメントと文字列に関する簡単な振り返り

コーディング演習1：パラメーターを定義する

セクション1.3：数学的操作

コーディング演習2：入力電流をシミュレーションする

セクション1.4：フォーマット済み文字列リテラル

コーディング演習3：綺麗な数値の表示

セクション2：`for`ループと離散時間積分

ビデオ3：`for`ループと離散時間積分

セクション2.1：`for`ループ

セクション2.2：スパイクによる離散時間積分

ビデオ4：離散時間積分の簡単な振り返り

コーディング演習4：膜電位のシミュレーション

セクション3：プロッティング

ビデオ5：プロッティング入門

ビデオ6：プロッティングの簡単な振り返り

コーディング演習5：電流のプロット